The Dual Mesh Finite Domain Method for the Convection–Diffusion Heat Equation and the Navier–Stokes
INTRODUCTION
The Dual Mesh Finite Domain Method (DMFDM), which was introduced in [1], divides a domain, Ω into grid of non-overlapping subdomains called the primal finite element mesh, or sometimes the primal mesh for short. This primal mesh of finite elements is then overlaid by a secondary mesh of node-centered control domains, which may occupy more than one finite element. The integral form of the equation, as opposed to a weak form or wegihted-residual statement, is evaluated over each node-centered control domain. In evaluating these integral forms, the values of primary and/or secondary variables are needed at the extremes of the control domain. The DMFDM takes advantage of the primary mesh of finite elements and uses their interpolation functions to provide values at the extremes of each control domain.
DISCRETIZING THE DOMAIN
The discretiztion for a 1-D domain of linear and quadratic primal elements are shown in Figures 1 and 2, respectively. The 1-D results can be seen presented in [2].
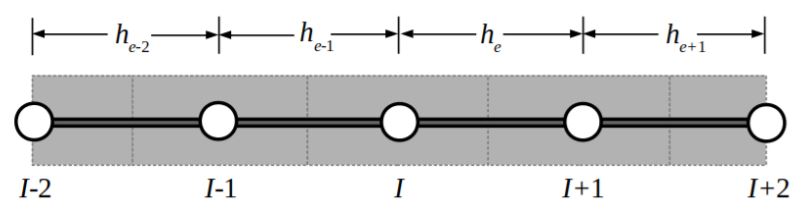
Fig. 1: Linear interpolations on both sides of the Ith control domain.
The same method is then expanded to 2-D, which can be seen in Figures 3 and 4. It is especially important to note that, for the quadratic grid, providing the coefficients for the Ith node will dpepend on the node’s location within the primal mesh. The value of the Ith node may depend on anywhere from 8 to 24 other nodes.
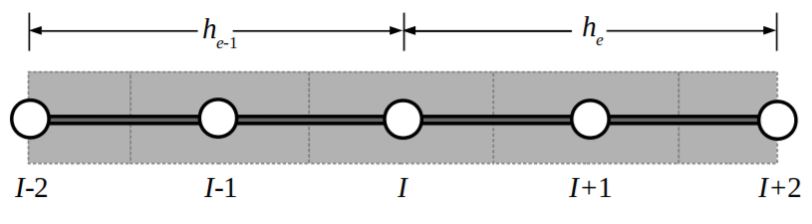
Fig. 2: Stencil of the Ith control domain about a node on the border of two elements in the quadratic primal mesh.
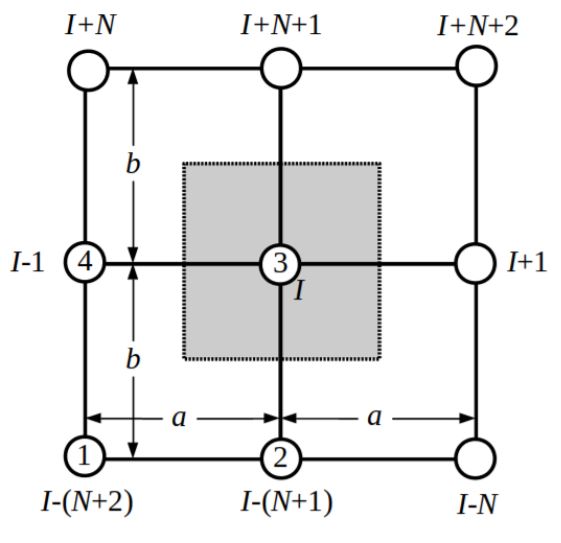
Fig. 3: Stencil for the linear 2-D DMFDM elements surrounding interior node I.
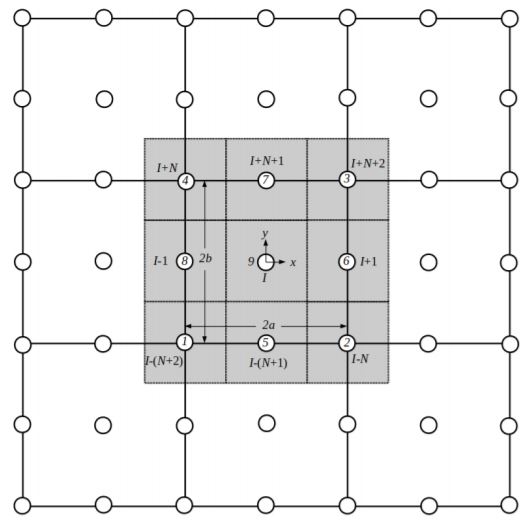
Fig. 4: Stencil for the quadratic 2-D DMFDM elements surrounding interior node I.
NUMERICAL RESULTS
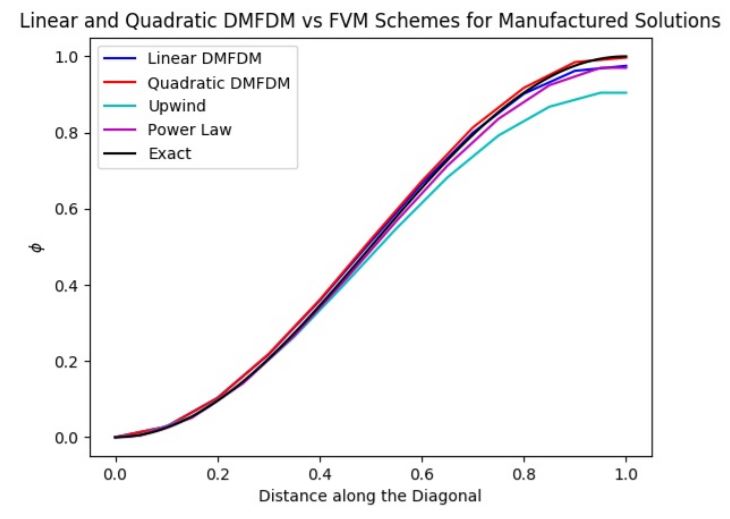
Fig. 5: Comparison between linear and quadratic 2D DMFDM and the Upwind and Power Law Finite Volume Methods.
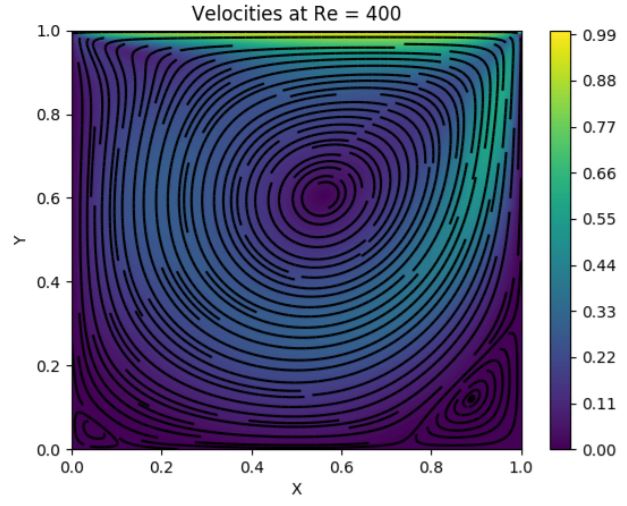
Fig. 6: Results for the 2-D linear DMFDM for the Navier–Stokes solution of the Lid Driven Cavity Problem.
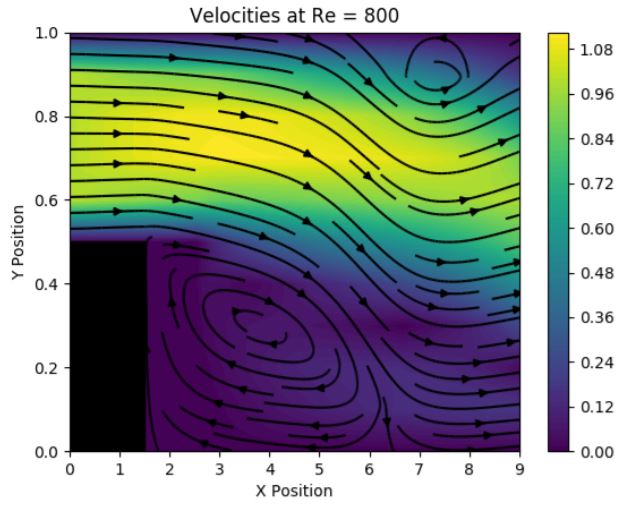
Fig. 7: Results for the 2-D linear DMFDM for the Navier–Stokes solution fo the flow over the backwards step.
References
[1] J. N. Reddy, ‘A dual mesh finite domain method for the numerical solution of differential equations,” International Journal of Computational Methods in Engineering Science and Mechanics, Vol. 20, No. 3, pp. 212-228, 2019.[2] J. N. Reddy, M. A. Martinez, ‘A Dual Mesh Finite Domain Method for SteadyState Convection–Diffusion Problems,” submitted to Computers and Fluids.
[3] J. N. Reddy, An Introduction to the Finite Element Method, 4th ed., McGraw– Hill, New York, NY, 2019.
[4] K. S. Surana and J. N. Reddy, The Finite Element Method for Boundary Value Problems, Mathematics and Computations, CRC Press, Boca Raton, FL, 2017.
[5] S. Patankar, Numerical Heat Transfer and Fluid Flow, CRC Press, Boca Raton, FL, 1980.
[6] H.K. Versteeg and W. Malalasekera, Computational Fluid Dynamics, The Finite Volume Method, 2nd ed., Pearson Education (Prentice–Hall), Harlow, England, UK, 2007.
[7] S. Mazumder, Numerical Methods for Partial Differential Equations. Finite Difference and Finite Volume Methods, Elsevier, New York, NY, 2016.
[8] J. N. Reddy, N. K. Anand, and P. Roy, The Finite Element and Finite Volume Methods in Heat Transfer and Fluid Dynamics, book manuscript in preparation, 2020.
[9] K. Salari, P. Knupp, ‘Code Verification by the Method of Manufactured Solutions,” United States: N. p., 2000. Web. doi:10.2172/759450.
