NONLINEAR FINITE ELEMENT ANALYSIS OF MICROPOLAR BEAMS AND PLATES

Praneeth Nampally, Anssi Karttunen, J.N. Reddy

INTRODUCTION

In micropolar continuum each point of the continuum is considered to be equivalent to a rigid body allowing each particle to have six degrees of freedom, three translations and three rotations (referred to as microrotations [1]). One of the applications of the micropolar theory is modelling lattice core sandwich beams and plates as an Equivalent Single Layer (ESL) micropolar beams [2] and plates. Here a geometrically nonlinear finite element model is developed for the bending analysis of micropolar Timoshenko beams and First Order Shear Deformation (FSDT) plates using the principle of virtual displacements[3]. Linear Lagrange interpolation functions are used in the interpolation of the respective degrees of freedom of beams and plates. The nonlinearity is included in the models by appending the linearized micropolar strain with von K´arm´an strain terms that allows the micropolar beams and plates to undergo moderate rotations.

 

DISPLACEMENTS, MICROROTATIONS AND STRAIN FIELDS

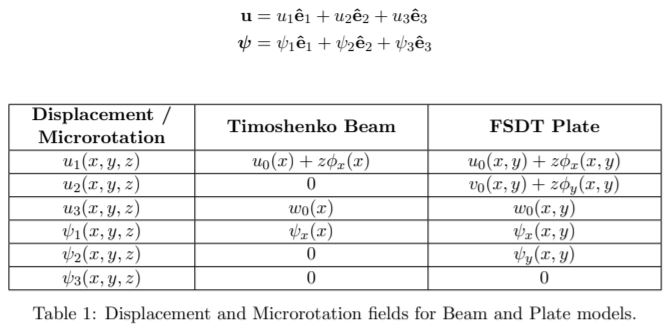
The displacement and microrotation in a micropolar continuum are given by

The definition of linearized microstrain and wryness tensors are

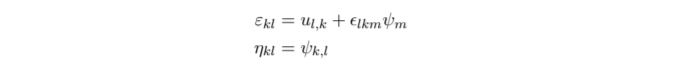
The governing equations and subsequently the finite element model are derived from the Hamilton’s principle [4]:

where K is the kinetic energy, U is the strain energy stored and V is the energy due to the external forces applied.

 

NUMERICAL RESULTS

Some of the numerical results for the web-core, Y-frame and hexagonal core beams are give below:

 

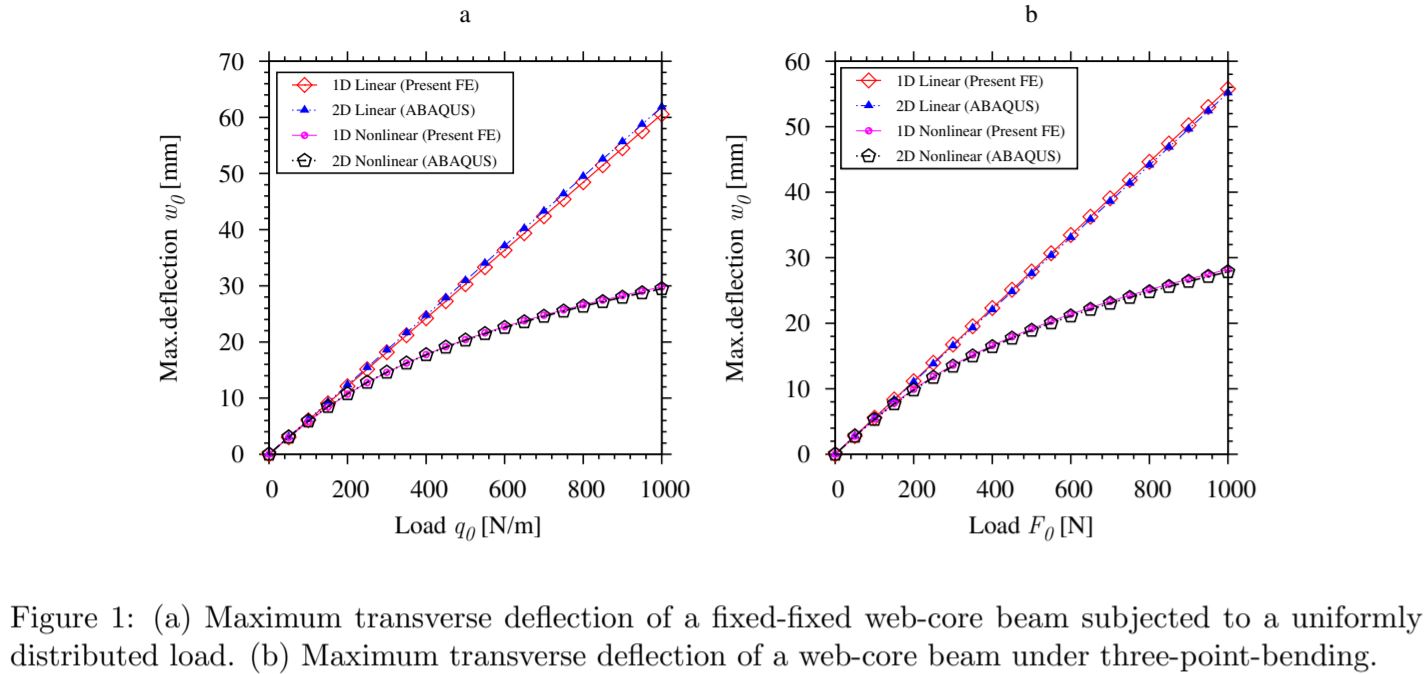
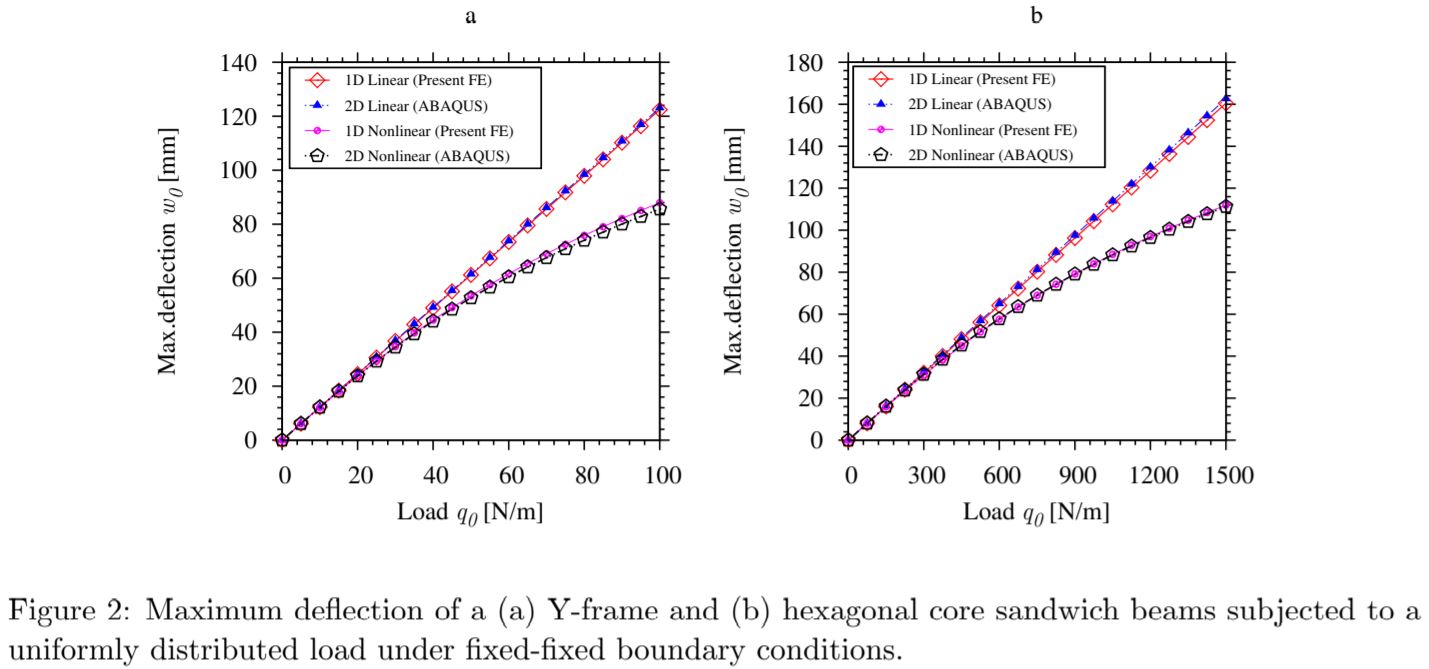
References

[1] Eringen, A. C., Suhubi, E. S., 1964. Nonlinear theory of simple micro-elastic solids, i and ii. Int. J. Eng. Sci., 2 (2),189–203.
[2] Karttunen, A. T., Reddy, J. N., Romanoff, J. 2018a. Micropolar modeling approach for periodic sandwich beams. Compos. Struct., 185, 656–664.
[3] Reddy, J. N., 2015. An Introduction to Nonlinear Finite Element Analysis, 2nd Edition. Oxford University Press, Oxford, UK.
[4] Reddy, J. N., 2017. Energy Principles and Variational Methods in Applied Mechanics, 3rd Edition. John Wiley& Sons, New York, NY.