Current Research Projects

A LAGRANGIAN BASED DIRECT APPROACH TO MACROSCOPIC MODELLING

A LAGRANGIAN BASED DIRECT APPROACH TO MACROSCOPIC MODELLING

Saikat Sarkat, Mohsen Nowruzpour, J. N. Reddy, and Arun Srinivasa

ABSTRACT

A direct Lagrangian based approach, designed at a length scale of interest, to characterize the response of a body is proposed. The main idea is to understand the dynamics of a deformable body via a Lagrangian corresponding to a coupled interaction of rigid particles in the reduced dimension (see [1,2] for more details).

EXPLORING NONLOCALITY

In the last decade there has been significant research activity in the use of Eringen’s nonlocal models [3] to reformulate the equations of beams and plates. All of the previous works used a length scale parameter to study its effect on bending, buckling, and vibration characteristics [4], without identifying what the length scale parameter means. An attempt is made herein, for the first time, to relate the length scale parameter(s) to physical parameters. The Eringen’s non-local Euler–Bernoulli and Timoshenko beam models are identified as continuum limits of a discrete system comprising of harmonic oscillators. The correspondence between the coefficients of the discrete and the continuum models is used to determine the source of the non-locality in the context of Eringen’s non-local beams [1].

Discrete energy

Figure 1. A System of harmonic oscillators.

Potential Energy

$\Pi _d = \sum_{j=2}^{N-1} T_j l_j (1 - \cos {\theta_j}) - \sum_{j=2}^{N} Q_j w_j$

Kinetic Energy

$K_d = \sum_{j=2}^{N-1} \left[ \frac{1}{2} M_0 v_j^2 + \sum_{i=-1}^{1} \frac{1}{2} M_2 \big( v_j - v_{j+i} \big)^2 + \sum_{i=-1}^{1} \frac{1}{2} I_2 \left( \frac{v_j - v_{j+i}}{h} \right)^2 + \frac{1}{2} I_0 \dot{\theta}_j^2 \right]$

Nonlocality parameters

$\mu _1^{EB}= \frac{2M_2 h^2}{M_0}, \; \mu _2^{EB}= \frac{I_0 h^2}{2 I_2}$

Via correspondence we can represent the nonlocality parameters in terms of variables in the discrete system (see Sarkar and Reddy [1] for details).

A DISCRETE LAGRANGIAN APPROACH TO MACROSCOPIC MODELLING

Here it is argued that the usual practice of describing the deformable body laws in the continuum limit is unnecessary, because for most of the practical problems, analytical solutions are not available. Since continuum limit is not taken, the framework automatically relaxes the requirement of differentiability of field variables. The discrete Lagrangian based approach can be applied to derive, for example, an equivalent Euler-Bernoulli beam model.

Figure 2: Evolution from reference configuration to deformed configuration

The Euler-Lagrange equations corresponding to $X_i$ may be arrived at as

(1) $\begin{equation*} \begin{align} \frac{\partial}{\partial t } \left( \frac{\partial \tau _i \big( \dot{\mathbf{u}}_i \big) }{\partial t } \right) V_i & + \sum_{j=1}^N \sum_{k=1}^N \frac{\partial}{\partial \mathbf{u}_i } \big(a_{jk} \omega _{ijk} \big) V_j V_k V_i + \sum_{j=1}^N \sum_{k=1}^N \frac{\partial}{\partial \mathbf{u}_i } \big(a_{ki} \omega _{jki} \big) V_j V_k V_i \\ & + \sum_{j=1}^N \sum_{k=1}^N \frac{\partial}{\partial \mathbf{u}_i } \big(a_{ij} \omega _{kij} \big) V_j V_k V_i = \mathbf{f}_i V_i \end{align} \end{equation*}$

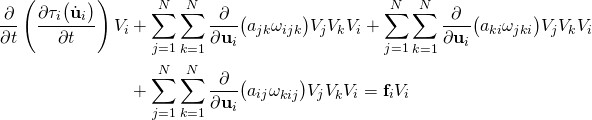
Bending characteristics may be incorporated in the discrete Lagrangian via:

(2) $\begin{equation*} \begin{align} \omega _{jki} & = \frac{1}{2} \beta \phi_{ki} \big( \boldsymbol{\theta }_{jki}^T \boldsymbol{\theta }_{jki} + \boldsymbol{ \Psi }_{jki} \big) \\ \omega _{kij} & = \frac{1}{2} \beta \phi_{ij} \big( \boldsymbol{\theta }_{kij}^T \boldsymbol{\theta }_{kij} + \boldsymbol{ \Psi }_{kij} \big) \\ \omega _{ijk} & = \frac{1}{2} \beta \phi_{jk} \big( \boldsymbol{\theta }_{ijk}^T \boldsymbol{\theta }_{ijk} + \boldsymbol{ \Psi }_{ijk} \big) \end{align} \end{equation*}$

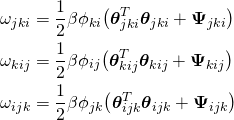
APPLICATION TO THE EULER-BERNOULLI BEAM

We design a discrete potential based on the notion of surface normal (see Figs. 3, 4 & 5) to model the Euler-Bernoulli beam.

Figure 3: Beam element and surface normal

Figure 4: Surface normal in two dimensions

Figure 5: Surface normal in three dimensions

With varying nonlocality parameter δ, we report the displacement profiles for three different cases: (1) simply supported (see Fig. 6), (2) clamped (see Fig. 7) and (3) cantilever (see Fig. 8) boundary conditions.

Figure 6: Displacement profiles with varying δ for cantilever beam

Figure 7: Displacement profiles with varying δ for simply support beam

Figure 8: Displacement profiles with varying δ for clamped beam

MICRO-CRACK PROPAGATION IN A THIN STRUCTURE

To show that we can simulate the problem of crack propagation on a thin isotropic plate (Figure. 9) and anisotropic plate (Figure. 10)) via an appropriate potential function.

Figure 9: Crack propagation in an isotropic plate

Figure 10: Crack propagation in an anisotropic plate

CONCLUSIONS

In this study, a suitable discrete Lagrangian based approach for solving dynamical systems at a length scale of interest is proposed. A major aspect of the work is to understand continuum nonlocality. It is argued that the usual practice of describing the deformable body laws in the continuum limit is redundant, because for most of the practical problems analytical solutions are not available.

ACKNOWLEDGEMENT

The authors gratefully acknowledge the support of this research by the Oscar S. Wyatt Endowed Chair funds.

REFERENCES

[1] Sarkar, S., & Reddy, J. N. (2016). Exploring the source of non-locality in the Euler–Bernoulli and Timoshenko beam models. International Journal of Engineering Science, 104, 110-115.
[2] Sarkar, S., Nowruzpour, M., Reddy, J. N., & Srinivasa, A. (2016). A Lagrangian Based Direct Approach to Macroscopic Modelling, Journal of the Mechanics and Physics of Solids, in review
[3] Eringen, A. C., & Edelen, D. G. B. (1972). On nonlocal elasticity. International Journal of Engineering Science, 10(3), 233-248.
[4] Reddy, J. N. (2007). Nonlocal theories for bending, buckling and vibration of beams. International Journal of Engineering Science, 45(2), 288-307.