Current Research Projects

A NON-LOCAL THIRD ORDER THEORY OF FUNCTIONALLY GRADED PLATES

A NON-LOCAL THIRD ORDER THEORY OF FUNCTIONALLY GRADED PLATES

Jinseok Kim and J.N. Reddy

INTRODUCTION

Plates are three-dimensional (3D) bodies that have much smaller dimension in the out-of-plane direction than the in-plane directions. To study behavior of these structural elements, it is efficient to reduce 3D problems to 2D problems because of geometrical characteristic of plate like bodies, the high computational costs and the complexity of the numerical analysis of 3D systems. The dimension can be reduced by separating volume integral into thickness(1D) and area (2D) integrals, and performing thickness integral first, the overall properties of a plate are represented by equivalent single layer (ESL) properties. The plate theories assume expansions of the field of dependent variables (stresses or displacements) through thickness directions based on hypotheses of each theories. With developments of novel material systems such as functionally graded materials, those theories should be extended to represent the new material systems. Since plates are fundamental elements of a structural system, they are often used in micro- and nano-scale structural systems which show size dependent effect in their mechanical responses. In this research, a general nonlinear third-order plate theory (GTPT) has been developed using the principle of virtual displacements [1-3]. The developed theory is based on geometric nonlinearity, size effects of structures in micro scale, functionally graded materials. The von Kármán nonlinear strains (i.e., small strain and moderate rotation) is considered to represent geometric nonlinearity. A modified couple stress theory is adopted to capture microstructure dependent size effect.

GENERAL THIRD ORDER PLATE THEORY

Displacement field

$\mathbf{u}_1 ( x,y,z,t ) & = u(x,y,t) + z \theta_x + z^2 \phi _x + z^3 \psi _x$

$\mathbf{u}_2 ( x,y,z,t ) & = u(x,y,t) + z \theta_y + z^2 \phi _y + z^3 \psi _y$

$\mathbf{u}_3 ( x,y,z,t ) & = u(x,y,t) + z \theta_z + z^2 \phi _z$

Dependent variables

$\theta_x = \left( \frac{\partial u_1}{\partial z} \right) _{z=0} \quad \theta_y = \left( \frac{\partial u_2}{\partial z} \right) _{z=0} \quad \theta_z = \left( \frac{\partial u_3}{\partial z} \right) _{z=0}$

$2\phi_x = \left( \frac{\partial^2 u_1}{\partial z^2} \right) _{z=0} \quad 2\phi_y = \left( \frac{\partial^2 u_2}{\partial z^2} \right) _{z=0} \quad 2\phi_z = \left( \frac{\partial^2 u_3}{\partial z^2} \right) _{z=0}$

$6 \psi _x = \frac{\partial^3 u_1}{\partial z^3} \quad 6 \psi _y = \frac{\partial^3 u_2}{\partial z^3}$

Principle of virtual displacement

$\int_0^T \left( \delta K - \delta U - \delta V \right) dt = 0$

Virtual kinetic energy

$\delta K = \int _{\Omega} \int^{h/2}_{-h/2} \rho \frac{\partial u_i}{\partial t} \frac{\delta \partial u_i}{\partial t} dz d \Omega$

Virtual strain energy

$\delta U = \int _{\Omega} \int^{h/2}_{-h/2} \left( \sigma_{ij} \delta \varepsilon_{ij} +m_{ij} \delta \chi _{ij} \right) dz d \Omega$

Virtual work done by external forces

(1) $\begin{equation*} \begin{align} \delta V = & - \left[ \int_V \left( \bar{f}_i \delta u_i + \bar{c}_i \delta \omega _i \right) dV + \int_S \left( \bar{t}_i \delta u_i + \bar{s}_i \delta \omega _i \right) dS \right. \\ & \left. + \int_{\Omega^t} \left( q^t_i \delta u_i + p^t_i \delta \omega _i \right) d \Omega ^t + \int_{\Omega^b} \left( q^b_i \delta u_i + p^b_i \delta \omega _i \right) d \Omega ^b \right] \end{align} \end{equation*}$

CONSTITUTIVE MODEL

Functionally graded materials

Functionally Graded Materials (FGMs) can be characterized by the gradual variation of material constituents over physical body, resulting in changes of the material properties, e.g. elastic modulus, mass density, thermal conductivity, and permittivity.

Variation of volume fraction of phase A through thickness of FGM plates.

Power Law Distribution of FGMs

$P(z) = (P_A - P_B) f(z) + P_B, \quad \text{where} \; f(z) = \left( \frac{1}{2} + \frac{z}{h} \right)^n$

MODIFIED COUPLE STRESS THEORY[5]

Strain Energy

$\mathbf{U} = \frac{1}{2} \int_V \big( \boldsymbol{ \varepsilon : \sigma } + \boldsymbol{ \chi : m} \big) = \frac{1}{2} \int_V \big( \sigma _{ij} \varepsilon_{ij} + m_{ij} \chi _{ij} \big) dV$

Curvature Tensor and Rotation Vector

$\boldsymbol {\chi } = \frac{1}{2} \left[ \boldsymbol{\nabla \omega } + \big( \boldsymbol{ \nabla \omega } \big) ^{\mathbf{T}} \right], \; \boldsymbol{ \omega } = \frac{1}{2} \boldsymbol{\nabla } \times \mathbf{u}$

Constitutive Relation

$\sigma _{ij} = 2 \mu \varepsilon _{ij} + \lambda \delta _{ij} \varepsilon _{kk}$

$m_{ij} = 2 \mu l^2 \chi _{ij}$

Equilibrium of a material particle system

Equivalence of forces.

jinseok-6

Equivalence of couple.

$\mathbf{F}' = \sum \mathbf{F}, \quad \mathbf{L}'=\sum(\mathbf{x}_i \times \mathbf{F}_i+ \mathbf{L}_i ), \quad \mathbf{M}' = \sum \mathbf{x}_i \times \mathbf{L}_i$

NUMERICAL EXAMPLE

Simply Supported Plate under UDL

Boundary conditions (constrained displacements and rotations)

jinseok-7

jinseok-8

jinseok-9

ACKNOWLEDGEMENT

The authors gratefully acknowledge the support of this work by the Air Force Office of Scientific Research through MURI Grant FA9550-09-1-0686 and the Oscar S. Wyatt Endowed Chair in Mechanical Engineering at Texas A&M University.

CONCLUSIONS

The developed plate theory presents plate thickness changes that provide three dimensional solution through two dimensional analysis.
The quadratic variation of transverse shear stress is promised and unlike first order shear deformation theory, a shear correction factor is not required.
The power-law index, n, can control stiffness of plates. In this example, smaller power-law index makes plate stiffer.
The developed plate theory has ability to capture the size effect of micro structure using length scale parameter, 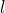$l$ ,of the modified couple stress theory.

REFERENCES

[1] J.N. Reddy and J. Kim, A nonlinear modified couple stress-based third-order theory of functional graded plates,” Composite Structures, 2012, 94: 1128-1143.
[2] J. Kim and J.N. Reddy, Analytical solutions for bending, vibration, and buckling of FGM plates using a couple stress-based third-order theory, Composite Structures, 2013, 103: 86–98.
[3] J. Kim, J.N. Reddy, A general third-order theory of functionally graded plates with modified couple stress effect and the von Karman nonlinearity: theory and finite element analysis, Acta Mechanica, 2015, 226 (9): 2973-2998.
[4] H. M. Yin, L. Z. Sun, and G. H. Paulino, Micromechanics-Based Elastic Model for Functionally Graded Materials With Particle Interactions, Acta Mater., 2004, 52: 3535–3543.
[5] F. Yang, A.C.M Chong , D.C.C. Lam, P. Tong, Couple stress based strain gradient theory for elasticity. Int J Solids Struct 2002, 39: 2731–43.