A TWELVE-PARAMETER SPECTRAL/HP SHELL FINITE ELEMENT FOR LARGE DEFORMATION ANALYSIS
ABSTRACT
A new 12-parameter shell finite element for large deformation analysis of shell structures is developed using third-order thickness stretch kinematics. The continuum shell element is utilized in the numerical simulations of isotropic, laminated composite and functionally graded materials, using a high-order spectral/hp approximations. The results obtained from the 12-parameter shell element are compared with those computed using a 7-parameter shell element to bring out the differences. The results show that the responses predicted by the two formulations are consistent with each other, with the 12-parameter model showing slight difference from those predicted by the 7-parameter model, specially for finite rotations.
INTRODUCTION
The classical shell elements generally include the hypothesis of a plane stress state and inextensibility of a transverse normal, and they are adequate in many applications involving small deformation. However, in applications where the deformations are large or there is a considerable change in the thickness of the shell they cannot reproduce the physical changes satisfactorily. To overcome this problem, new shell finite element formulations have been developed. These formulations also take into account the change in thickness and can be used to model thin and thick shells.
One of these formulations is the so called 7-parameter formulation, where the transverse displacement is expanded up to quadratic terms, and the Poisson locking can be mitigated when three dimensional constitutive equations are adopted. A tensor-based finite element shell with first-order shear deformation theory and seven parameters had been explored by Arciniega and Reddy [1], Payette and Reddy [2], and Gutierrez Rivera and Reddy [3]. The use of high-order plate and shell theories have also been explored, where the nonlinear terms in the normal and in plane displacements are retained. Recently, Amabili [4] introduced a geometrically nonlinear shell theory allowing third-order thickness stretch, higher-order shear deformation, and rotary inertia by using eight independent parameters. Inspired in this work, Gutierrez Rivera et al. [5] presented a new 12-parameter shell finite element for large deformation analysis of shell using third-order thickness stretch kinematics.
METHODOLOGY
A finite element approximation of the mid-surface is used, leading to the following finite element approximation at an element level:
(1) 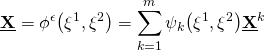
where ![]() is the approximate mid-surface coordinates,
is the approximate mid-surface coordinates, ![]() are the two-dimensional spectral/hp basis functions associated with the
are the two-dimensional spectral/hp basis functions associated with the ![]() node,
node, ![]() is the number of nodes in the element, and
is the number of nodes in the element, and ![]() are the element nodal coordinates with respect to a fixed orthogonal Cartesian coordinate system.
are the element nodal coordinates with respect to a fixed orthogonal Cartesian coordinate system.
At each point of the mid-surface we define the local basis vectors of the tangent plane ![]() and, instead of using the unit normal vector definition, we utilize its finite element approximation
and, instead of using the unit normal vector definition, we utilize its finite element approximation ![]() . The position vector in the shell element can be described, assuming a constant thickness
. The position vector in the shell element can be described, assuming a constant thickness ![]() , as
, as
(2) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{align} \mathbf{X}= \Phi ^e \big( \xi^1, \xi^2, \xi^3 \big) & = \boldsymbol{ \phi }^e \big( \xi^1, \xi^2 \big) + \xi^3 \frac{h}{2} \hat{\mathbf{n}} \big( \xi^1, \xi^2 \big) \\ & \xi^3 \in \big[ -1,1\big] \end{align} \end{equation*}](https://mechanics.tamu.edu/wp-content/ql-cache/quicklatex.com-0187839f6701d62549982f9672185aa0_l3.png)
The displacement of a material point ![]() from the reference configuration to a point
from the reference configuration to a point ![]() in the current configuration may be expressed as
in the current configuration may be expressed as ![]() , where
, where ![]() represent the mapping of the shell from the reference to the current configuration. We assume that the displacement vector at any point within the shell element can be approximated by the following twelve parameter expansion:
represent the mapping of the shell from the reference to the current configuration. We assume that the displacement vector at any point within the shell element can be approximated by the following twelve parameter expansion:
(3) ![]()
Using the displacement field proposed, the Green-Lagrange strain tensor ![]() is computed, and their covariant components can be expanded as a function of the thickness coordinate
is computed, and their covariant components can be expanded as a function of the thickness coordinate ![]() up to sixth grade. However, in this formulation, we neglect all the cubic and higher-order terms.
up to sixth grade. However, in this formulation, we neglect all the cubic and higher-order terms.
Since we only analyze the mechanical response for elastic shells, we assume that the relation between the second Piola-Kirchhoff stress tensor ![]() and the Green-Lagrange strain tensor
and the Green-Lagrange strain tensor ![]() is linear, and it is described by
is linear, and it is described by ![]() , where
, where ![]() is the fourth-order elasticity tensor and it is assumed to be independent of the shell deformation.
is the fourth-order elasticity tensor and it is assumed to be independent of the shell deformation.
We use the principle of virtual displacements to construct the finite element model. In the numerical implementation we employ a high-order spectral/hp finite element approximations, and we use the Gauss-Legendre quadrature rule with 50 quadrature points through the thickness direction to obtain nearly exact values. We apply Newton’s method for solving the resulting nonlinear set of algebraic equations.
NUMERICAL RESULTS
We present here some results obtained using the model. In all the graphs, the continuous and dashed lines stand for the 7- and 12-Parameter shell models, respectively. Figure 1 shows how the element presented is capable to reproduce the change of thickness in a simply supported isotropic plate under uniformly distributed load. The results are compared with an analytical solution.

Figure 1 (a) Thickness deformation.

Figure 1 (b) Normal displacement across the thickness.

Figure 1 (c) Deformed configuration.
Figure 2 shows how this element can reproduce the post-buckling response of laminated composite plate under a compressive load. The results are compared with some experimental data reported in [6].

Figure 2 (a) Normalized end shortening deflections versus dimensionless load.

Figure 2 (b) Normalized out of plane deflection versus dimensionless load.

Figure 2 (c) Deformed configuration of a laminated plates after buckling.
Figure 3 illustrates the behavior of a clamped functionally graded strip plate subjected to a bending distributed moment on the free end. This example is used to test the capability to simulate finite rotations.

Figure 3: (Left) Deformed configurations of a functionally graded cantilever plate strip, for ![]() . (Right) End moment vs. tip-deflection
. (Right) End moment vs. tip-deflection ![]() .
.
CONCLUSIONS
We find that the 12-parameter shell element performs better than the 7-parameter shell element. The change in thickness is more accurate using the 12-parameter formulation, specially near to the edges. Both formulations have excellent agreement with the experimental results for composite plates. For finite rotations, we observe a better behavior for 12-parameter formulation, giving more smooth curves after it reaches the high tip displacement for functionally grade plates. For these reasons, the 12-parameter formulation should be used when more accurate results are desired in large deformation and finite rotation analysis.
REFERENCES
[1] G.S. Payette, J.N. Reddy, A seven-parameter spectral/hp finite element formulation for isotropic, laminated composite and functionally graded shell structures, Comput. Methods Appl. Mech. Eng. 278 (2014) 664-704.[2] R.A. Arciniega, J.N. Reddy, Tensor-based finite element formulation for geometrically nonlinear analysis of shell structures, Comput. Methods Appl. Mech. Eng. 196 (2007) 1048-1073.
[3] M. Gutierrez Rivera, J.N. Reddy, Stress analysis of functionally graded shells using a 7-parameter shell element, Mechanics Research Communications, to appear (2016), http://dx.doi.org/10.1016/j.mechrescom.2016.02.009.
[4] M. Amabili, Non-linearities in rotation and thickness deformation in a new third-order thickness deformation theory for static and dynamic analysis of isotropic and laminated doubly curved shells, Int. J. Non-Linear Mech. 69 (2015) 109-128.
[5] M. Gutierrez Rivera, J.N. Reddy, M. Amabili, A new twelve-parameter spectral/hp shell finite element for large deformation analysis of composite shells, Compos. Struct. , 151 (2016) 183-196.
[6] J. H. Starnes Jr and M. Rouse, Postbuckling and failure characteristics of selected at rectangular graphite-epoxy plates loaded in compression, AIAA paper, 81 (1981) 423-434.
ACKNOWLEDGEMENTS
The first author wishes to acknowledge the financial support of the Mexican government through the “Consejo Nacional de Ciencia y Tecnologia” (CONACYT) and the “Secretaria de Educacion Publica” (SEP).
