Novel Ultrasound Elastography Technique for Cancer Diagnosis
ABSTRACT
Interstitial fluid pressure (IFP) represents a main factor in tumor growth and therapeutic efficiency. This becomes more important in solid tumors which show an elevated IFP compared with healthy tissues. In this research, a clinically relevant model is proposed for ultrasound elastography which can predict volumetric strain and interstitial fluid pressure in tumors. A biomechanical biphasic model for spherical tumorssurrounded by normal tissues is established.
INTRODUCTION
It has been documented that the interstitial fluid pressure (IFP) of most solid tumors is relatively high compared with normal tissues [1, 2]. The elevated tumor IFP is attributable to high blood vessel permeability, low lymphatic drainage, interstitial fibrosis and a contraction of the interstitial space mediated by stromal fibroblasts [2, 3]. Therefore, the IFP can be used as a biomarker for cancer diagnosis and prognosis [2]. However, clinical use of IFP has been limited due to the lack of noninvasive methods for its measuring [4]. So, establishing a noninvasive method to measure tumor IFP would be valuable in tumor diagnosis and prognosis. Increased tumor IFP obstacles transcapillary convective transport, so it lowers drug delivery to the targeted tumor cells, reducing the therapeutic efficiency [5], in addition, it causes metastatic dissemination [6].
Ultrasound elastography (USE) is a non-invasive medical imaging modality that was developed in the 1990s [7] which can create images of tissue stiffness by measuring tissue elastic properties. USE can be categorized into two main types based on the measured physical quantity: strain and shear wave [8, 9]. Strain elastography (SE) where the displacement of the tissue due to the application of a transducer external force or physiological force (breathing or heartbeat) is measured. Shear wave elastography (SWE) where the tissue stiffness can be measured based on the shear wave velocity propagating through the tissue [10].
MATHEMATICAL MODEL
The basic principle of this technique is based on measuring the axial displacement in the lesion by applying an external force as shown in Figure 1.
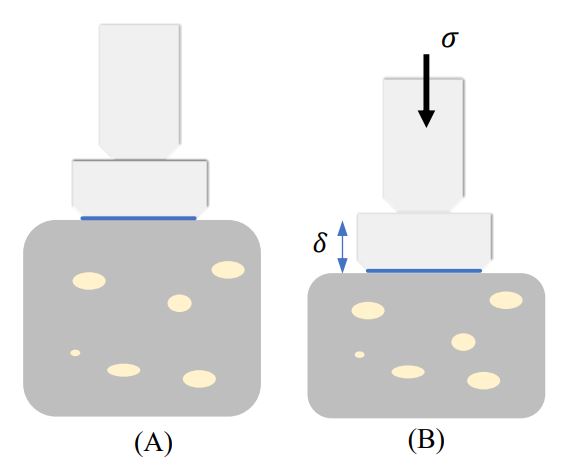
Figure 1: Static Elastography principle: tissue under compressive stress (σ). (A) tissue before compression, (B) tissue after compression
The proposed model can be represented as a biphasic spherical tumor surrounded by normal tissues under axial loading as shown in Figure 2(A).
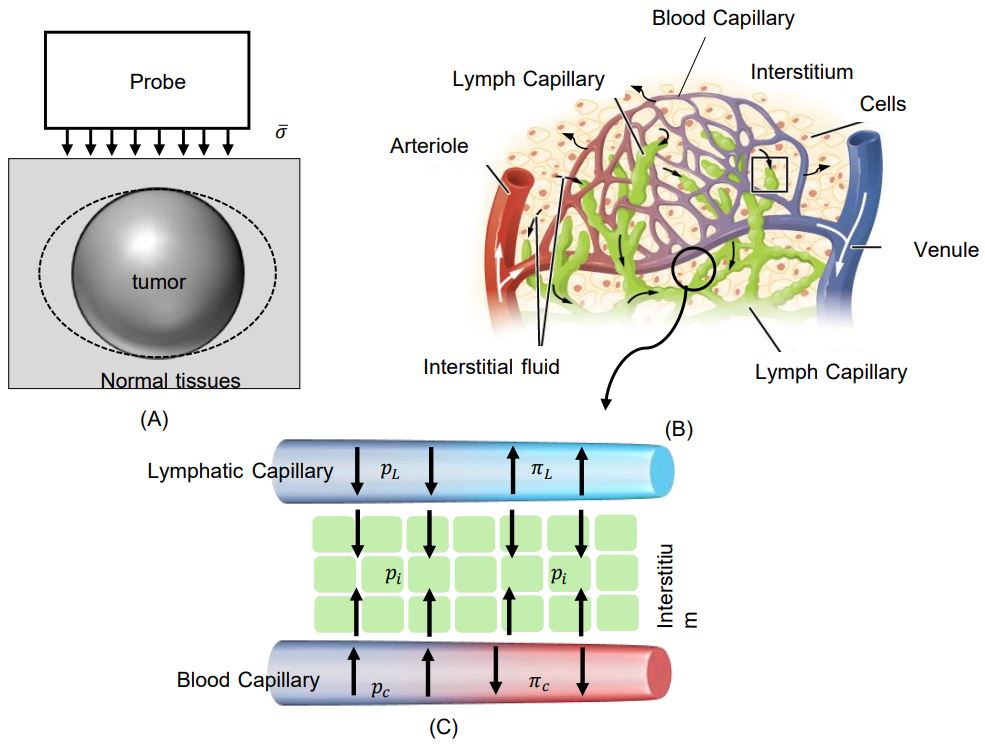
Figure 2: (A) A schematic description of spherical tumor under static elastography test. (B) A schematic of spherical tumor with applied stress. (C) A Schematic representation of the Interstitial fluid exchange based on Starling principle
RESULTS
The mathematical model was solved using COMSOL. For a tumor with diameter 4 𝑚𝑚, the radial profile of IFP corresponding to different normalized time points is shown in Figure 4. It can be noticed that the predicted tumor IFP profiles are uniform and high at the tumor center and drop to the lowest at the periphery and they match well with experimental observations of [11]. On the other hand, it can be noticed that IFP increased over time as shown in Figure 3, which would be consistent with the results of [12, 13].
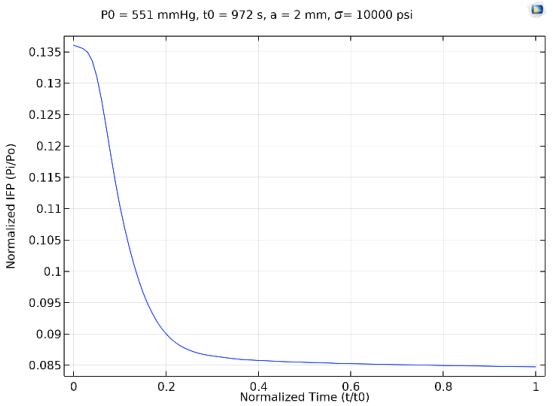
Figure 3:Time Profile of Normalized Tumor IFP at r/a=0.1
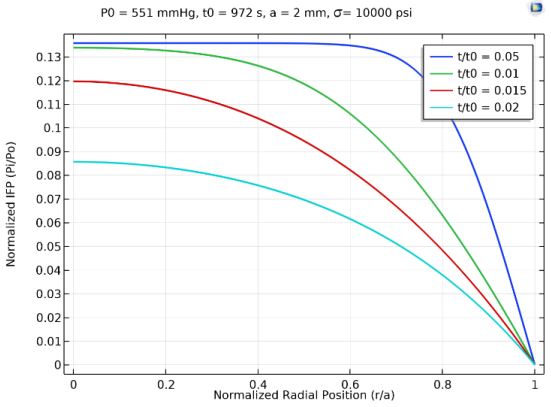
Figure 4: Radial Profiles of the Normalized Tumor IFP for Different Normalized time points
References
[1] Lunt, S.J., et al., Interstitial fluid pressure in tumors: therapeutic barrier and biomarker of angiogenesis. 2008.[2] Ferretti, S., et al., Tumor interstitial fluid pressure as an early-response marker for anticancer therapeutics. Neoplasia, 2009. 11(9): p. 874-881.
[3] Heldin, C.-H., et al., High interstitial fluid pressure—an obstacle in cancer therapy. Nature Reviews Cancer, 2004. 4(10): p. 806-813.
[4] Liu, L.J., et al., Estimation of tumor interstitial fluid pressure (tifp) noninvasively. PloS one, 2016. 11(7): p. e0140892.
[5] Stylianopoulos, T., L.L. Munn, and R.K. Jain, Reengineering the physical microenvironment of tumors to improve drug delivery and efficacy: from mathematical modeling to bench to bedside. Trends in cancer, 2018. 4(4): p. 292-319.
[6] Hompland, T., et al., Interstitial fluid pressure and associated lymph node metastasis revealed in tumors by dynamic contrast-enhanced MRI. Cancer research, 2012. 72(19): p. 4899-4908.
[7] Gennisson, J.-L., et al., Ultrasound elastography: principles and techniques. Diagnostic and interventional imaging, 2013. 94(5): p. 487-495.
[8] Nowicki, A. and K. Dobruch-Sobczak, Introduction to ultrasound elastography. Journal of ultrasonography, 2016. 16(65): p. 113.
[9] Correas, J.-M., et al., Ultrasound elastography of the prostate: state of the art. Diagnostic and interventional imaging, 2013. 94(5): p. 551-560.
[10] Dietrich, C.F., et al., Strain elastography-how to do it? Ultrasound international open, 2017. 3(04): p. E137-E149.
[11] Boucher, Y., L.T. Baxter, and R.K. Jain, Interstitial pressure gradients in tissue-isolated and subcutaneous tumors: implications for therapy. Cancer research, 1990. 50(15): p. 4478-4484.
[12] Stylianopoulos, T., et al., Coevolution of solid stress and interstitial fluid pressure in tumors during progression: implications for vascular collapse. Cancer research, 2013. 73(13): p. 3833-3841.
[13] Sarntinoranont, M., F. Rooney, and M. Ferrari, Interstitial stress and fluid pressure within a growing tumor. Annals of biomedical engineering, 2003. 31(3): p. 327-335.
