Current Research Projects

DISCRETIZED APPROACH FOR THE STUDY OF DAMAGE

GraFEM: A DISCRETIZATION APPROACH FOR STUDY OF DAMAGE AND FRACTURE IN SOLIDS

P. Khodabakshi, H. Y. Shin, P. Thamburaja, A. R. Srinivasa, and J. N. Reddy

Objective

Engineers are not just concerned with the design and construction of structures, but they also need to be able give an estimate of the life-span of a structure and predict how and when the structure will be damaged. Due to the amount of uncertainty involved, damage mechanics is one of the most complicated concepts in computational mechanics and is one of the most critical areas of research. To this end, we propose a new approach to damage analysis with the use of the conventional finite element method.

The finite element method is without doubt the most widely used computational framework in the field of applied mechanics. The target is to avoid the complexities involved in the approaches previously introduced so that the method is practically applicable for engineering design purposes.

Background

There exist several approaches in the literature on the study of damage in materials. The most common are listed in the following:

Fracture Mechanics
Continuum Damage Mechanics
Lattice Models
Extended Finite Element Method
Nonlocal Theories

Any numerical or analytic technique suffers from some weaknesses. Fracture mechanics, as initially introduced in the studies by Griffith [1] and Irwin [2] is only limited to study of a single crack with a pre-specified location. Therefore, it is incapable of predicting nucleation and growth of new cracks, or branching of existing cracks. Cohesive zone models, which are considered nonlinear fracture mechanics, are capable of capturing nucleation of cracks; however, one needs to determine the areas of probable cracks in advance to enrich them with cohesive models and continuous remeshing is required. Continuum damage mechanics (CDM), as introduced by Kachanov [3], is a robust method in studying damage evolution, however the method only gives a homogenized characteristic of a representative volume element (RVE) for randomly dispersed microdefects. Evolution of cracks cannot be studied using CDM. Lattice models require a technique to discretize a continuum into a network of either beams or trusses with overall physical properties similar to the original continuum. This technique is usually not very straightforward, and in order to represent the continuum with good accuracy it requires a huge network of elements. Peridynamic theory, which is a nonlocal theory recently proposed by Silling [4], is only limited to a Poisson’s ratio of 0.25 in its original formulation (bond-based peridynamic theory). This is a serious limitation even in the case of isotropic elasticity where the solution depends upon the material parameters only through the Poisson’s ratio. The limitation was later removed by the introduction of state-based peridynamic theory [5]. However, the non-ordinary state-based peridynamic theory is ill-conditioned in the sense of satisfying balance of angular momentum. Also the complexity of the method prevents it from becoming applicable for design purposes.

In all of the above mentioned theories an external failure criterion should be imposed to be able to study the evolution and growth of damage. In this study an approach is introduced where damage can naturally be accounted for by using the conventional finite element method. This will be very beneficial because FEM is the most widely used numerical method in computational mechanics.

Technical Approach

The proposed method is based on the study by Reddy and Srinivasa [6] where it is shown that for hyperelastic materials the nodal forces of a discretized domain are directed along the edges of the element. Furthermore, the value of these forces can be expressed in terms of the strains along the edges of the element. To illustrate this idea, assume a linear triangular element in a two-dimensional isotropic plane elasticity problem, as shown below. The strain energy density function for this element can be written as:

$U_0=U_0 ( \varepsilon _{xx},\varepsilon _{yy},\varepsilon _{zz}) = \frac{1}{2} \big\{ c_{11} \varepsilon _{xx}^2 + c_{22} \varepsilon _{yy}^2 +2c_{12} \varepsilon_{xx} \varepsilon_{yy} + c_{66} \gamma _{xy}^2 \big\}$

Displacements and normal strains in the direction of the edges of the element

Normal strains along the edges of the element can be derived by transforming the strains $\varepsilon _{xx}$ , $\varepsilon _{yy}$ , and $\gamma _{xy}$ .

$\begin{bmatrix} \varepsilon _1 \\ \varepsilon _2 \\ \varepsilon _3 \end{bmatrix} = \mathbf{T} \begin{bmatrix} \varepsilon _{xx} \\ \varepsilon _{yy} \\ \gamma _{xy} \end{bmatrix}, \; \mathbf{T}= \begin{bmatrix} \frac{1}{L_1^2} & 0 & 0 \\ 0 & \frac{1}{L_2^2} & 0 \\ 0 & 0 & \frac{1}{L_3^2} \end{bmatrix} \begin{bmatrix} \gamma_1^2 & \beta_1^2 & -\gamma_1 \beta_1 \\ \gamma_2^2 & \beta_2^2 & -\gamma_2 \beta_2 \\ \gamma_3^2 & \beta_3^2 & -\gamma_3 \beta_3 \end{bmatrix}$

Using the transformation equation, the strain energy density function can be rewritten in terms of normal strains along the edges of the triangular element:

$U_0=U_0 ( \varepsilon _{1},\varepsilon _{2},\varepsilon _{3}) = A_{11} \varepsilon _1^2 + A_{22} \varepsilon _2^2 + A_{33} \varepsilon _3^2 + A_{12} \varepsilon _1 \varepsilon _2 + A_{23} \varepsilon _2 \varepsilon _3 + A_{31} \varepsilon _3 \varepsilon _1$

where coefficients $A_{ij}$ depend only on the geometry of the element and material properties. Using the previous equation, the damage variable $\phi _i$ can be assigned to the normal strain $\varepsilon _i$ . In other words $\phi _i$ represents the extent to which side $i$ can withstand forces. The previous equation can be rewritten as:

(1) $\begin{equation*} \begin{align} U_0^d & = U_0^d ( \phi _1 \varepsilon _1, \phi _2 \varepsilon _2, \phi _3 \varepsilon _3) \\ & = A_{11} \big( \phi _1 \varepsilon _1 \big) ^2 + A_{22} \big( \phi _2 \varepsilon _2 \big) ^2 +A_{33} \big( \phi _3 \varepsilon _3 \big) ^2 \\ & \quad + A_{12} \phi _1 \varepsilon _1 \phi _2 \varepsilon _2 + A_{23} \phi _2 \varepsilon _2 \phi _3 \varepsilon _3 + A_{31} \phi _3 \varepsilon _3 \phi _1 \varepsilon _1 \end{align} \end{equation*}$

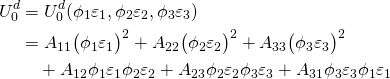
The strain energy density function can be used to derive the stiffness matrix in the damaged state:

$\mathbf{K}^d = h \mathbf{A} \mathbf{B}^T \mathbf{T}^T \boldsymbol{ \Phi } \mathbf{T}^{-T} \mathbf{C} \mathbf{T}^{-1} \boldsymbol{ \Phi } \mathbf{T} \mathbf{B}$

where $\mathbf{B}$ is the matrix relating the displacements to strains [7], $\mathbf{T}$ the transformation matrix, $\boldsymbol{ \Phi }$ the diagonal damage matrix (with $\phi_i$ ’s located on the diagonal), and $\mathbf{C}$ the elasticity matrix.

Numerical Examples

To numerically study the applicability of the proposed method, a simple damage criterion is used:

$\phi _i = \begin{cases} 1 & \quad \varepsilon _i \leq \varepsilon _{critical} \\ 0 & \quad \varepsilon _i > \varepsilon _{critical} \\ \end{cases}$

For the damage criteria, the tensile strength of material is used. If the stress value at the edge reaches a critical value(tensile strength), then the edge is considered as a broken edge. The developed model of damage implemented in ABAQUS as VUMAT subroutine to incorporate the dynamic analysis capability.

Below shows the numerical example of quasi-brittle fracture behavior of material. The domain of analysis is a discretized rectangular plate with a circular hole. For speed up the analysis, the symmetry of the domain was considered and the simulation was done for the half of domain. As for the boundary condition, the plate was constrained in the vertical direction along the bottom surface. The load was given as velocity input on the top surface with very low speed to meet the criteria of quasi brittle fracture.

The average of damage variable for each element is described as SDV2 and true stress value in Y direction is having state variable name as SDV7. True stress is the stress value incorporating the damage variable. The left pane at the below video shows how crack propagate through the domain as the abrupt fracture occurred after the peak force value. The right pane shows the distribution of the true stress in Y direction. The video shows the results from the point where the top surface displacement at 0.0348m.

Damage zone propogation(left) and true stress distribution in Y direction(right)

The below picture shows the force-displacement graph at the top surface. The force value dropped to nearly zero value almost immediately after it reached peak value.

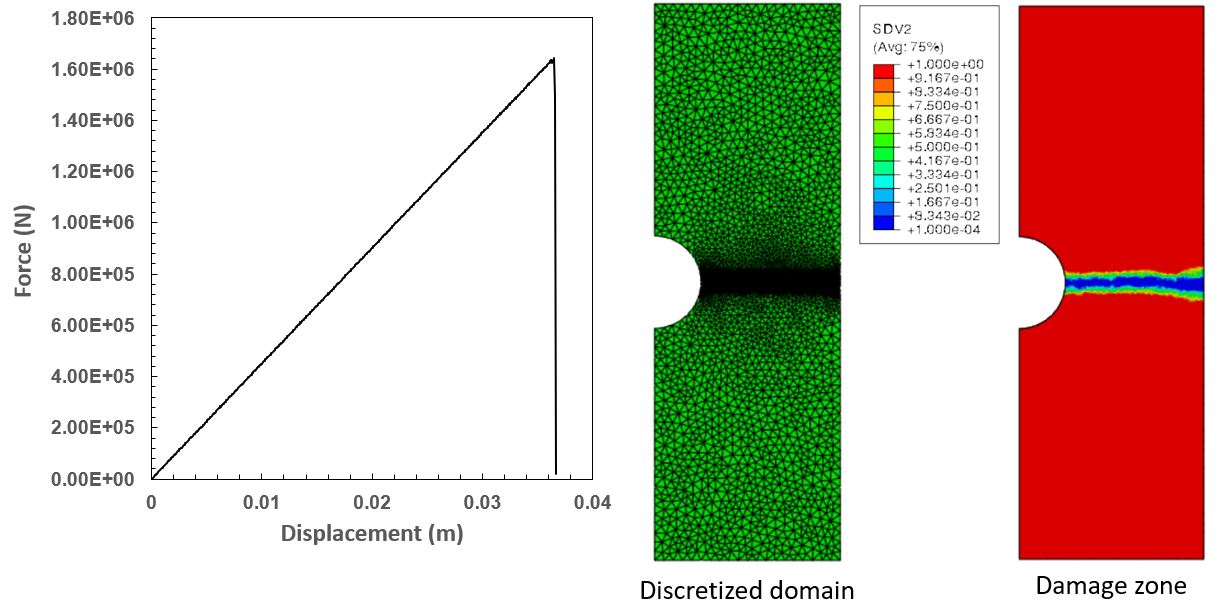
Force-displacement graph on top surface

Conclusions

A new approach to study of damage within materials is introduced based on the study by Reddy and Srinivasa [6]. Since the forces and strains in a hyperelastic material can be written along the edges of the elements, a damage criterion can be imposed either on the normal forces or normal strains directed along the edges of the elements.

References

[1] A.A. Griffith. The phenomena of rupture and flow in solids. Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 221(582-593):163–198, 1920.
[2] G.R. Irwin. Analysis of stresses and strains near the end of a crack traversing a plate. ASME Journal of Applied Mechanics, 24:361–364, 1957.
[3] L.M. Kachanov. Time of the rupture process under creep conditions. Izv. Akad. Nauk. S.S.R. Otd. Tech. Nauk., 8:26–31, 1958.
[4] S.A. Silling. Reformulation of elasticity theory for discontinuities and long-range forces. Journal of the Mechanics and Physics of Solids, 48(1):175–209, 2000.
[5] S. A. Silling, M. Epton, O. Weckner, J. Xu, and E. Askari. Peridynamic states and constitutive modeling. Journal of Elasticity, 88(2):151–184, 2007.
[6] J.N. Reddy and A. Srinivasa. On the force displacement characteristics of finite elements for elasticity and related problems. Finite Elements in Analysis and Design, 104:35 – 40, 2015.
[7] J.N. Reddy. Energy Principles and Variational Methods in Applied Mechanics, Second Edition. John Wiley & Sons, New York, NY, 2002.
[8] P. Khodabakhshi and J.N. Reddy. New approach to damage mechanics through a modified finite element framework. Paper presented to Engineering Mechanics Institute Conference 2016 (EMI2016), Nashville, TN, 2016.