TAMU Mechanics

Current Research Projects

LEAST-SQUARES FINITE ELEMENT ANALYSIS OF FLOWS OF VISCOUS, INCOMPRESSIBLE, GENERALIZED NEWTONIAN FLUIDS

Namhee Kim and J.N. Reddy

BACKGROUND

Least-squares finite element model (LSFEM)

  • Alternative method to conventional weak-form Galerkin finite element model for fluid problems.
  • Minimizing the sum of squared norms of the residuals in governing equations. The basic ides is given below.

    • Given an operator equation of the form

        \[ A(u) = f \; \text{in} \; \Omega \quad \text{and} \quad B(u) = g \; \text{in} \; \Gamma \]

    we seek suitable approximation of u as u_h. In the least-squares method, we seek the minimum of the sum of squares of the residuals in the approximation of the equations:

        \[ 0 = \delta I(u_h) = \delta \int_{\Omega} \left[ A(u_h) - f \right]^2 dx + \delta \oint_{\Omega} \left[ B(u_h) - g \right]^2 ds \]

LSFEM’s advantages for Navier–Stokes equations

  • Variational framework for the Navier–Stokes equations (minimization problem)

    -Free of restrictive compatibility condition.

    -Same but higher-order interpolation functions.

  • No need a numerical diffusion.
  • For linear partial differential equations, symmetric positive-definite (SPD) coefficient matrices regardless of symmetry in the governing equations.

    -Linearize the Navier–Stokes equations.

LSFEM’s deficiencies & remedies

  • Higher regularity of the approximate solution; negative effects on the conditioning of coefficient matrices and convergence of solution.

    -Equivalent first-order system of governing equations with auxiliary variables (stress or velocity gradient).

  • Weak in local mass conservation for both steady and unsteady flow problems.

    -Weighting the residual of continuity equation, Higher polynomial order of approximations, Least-squares functional with volumetric flow imbalance.

  • Locking problem in low-order LSFEMs for non-H1-coercive formulation in terms of a priori estimate.

    -Selective reduced integration methods, High-order approximations, High-order spectral/hp approximations.

Spectral vs. Lagrange interpolation functions

namhee-1

OBJECTIVE

Develop a least-squares finite element model with high-order spectral/hp approximations for steady flows of generalized Newtonian fluids obeying Carreau–Yasuda viscosity model.

LEAST-SQUARES FORMULATION

Least-squares functional

    \[ \mathcal{J} (p, \mathbf{v}, \underline{\boldsymbol{ \tau }}, \theta, \mathbf{q} ) = \frac{1}{2} \left( \parallel R_1 \parallel^2_{\Omega,0} + \parallel R_2 \parallel^2_{\Omega,0} + \parallel R_3 \parallel^2_{\Omega,0} \right) \]

(1)   \begin{equation*} \begin{align} & R_1 = \nabla \cdot \mathbf{v} \\ & R_2 = \mathbf{v} \cdot \nabla \mathbf{v} + \nabla p - \nabla \cdot \underline{\boldsymbol{ \tau }} \\ & R_3 = \underline{\boldsymbol{ \tau }} - \mu \left( \nabla \mathbf{v} + \nabla \mathbf{v}^T \right) \end{align} \end{equation*}

    \[ \ast \mu(I_2) = \frac{1}{Re} \left\{ \mu_{ \infty } + (\mu_0 - \mu_{ \infty }) \left[ 1 + \left( \lambda _{CY} {I_2}^{ 1/2 } \right)^a \right]^{ \frac{n-1}{a} } \right\} \]

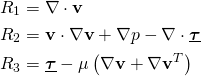
Linearization before minimization

Linearize nonlinear operators in \mathcal{J}: using Newton’s method (\mathcal{J} \rightarrow \mathcal{J} _{Lin})

Minimization problem ( \delta \mathcal{J} _{Lin} =0)

Find \mathbf{u} = (p, \mathbf{v}, \underline{\boldsymbol{ \tau }}) \in \mathcal{V}, such that \mathcal{B} (\mathbf{u}, \delta \mathbf{u}) = \mathcal {F} (\delta \mathbf{u}) \forall \delta \mathbf{u} = (\delta p, \delta \mathbf{v}, \delta \underline{\boldsymbol{ \tau }}) \in \mathcal{V} (\mathcal{B}: bilinear form, \mathcal{F}: linear form).

NUMERICAL RESULTS

Flow over a backward-facing step

namhee-2
namhee-3
namhee-4

Code validation by experimental results (laminar flow) of Armaly et al.(1983)

namhee-5

Parametric study on Carreau-Yasuda fluids: Effect of a

namhee-6

Parametric study on Carreau-Yasuda fluids: Effect of n

namhee-7

Parametric study on Carreau-Yasuda fluids: Effect of \lambda _{CY}

namhee-8

Lid-driven cavity flow

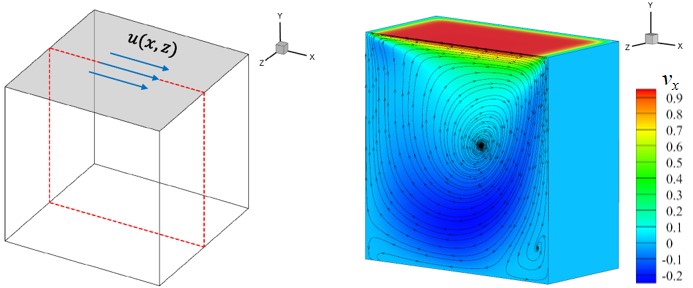
namhee-8

Fig. 1. Schematic of the lid-driven cavity flow problem.

 

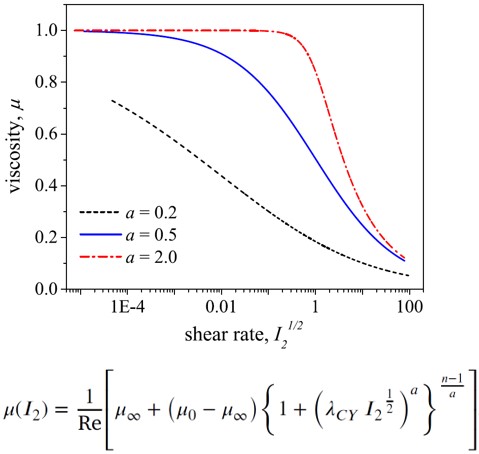
namhee-8

Fig. 2. Effect of the shape parameter, a, on the viscosity ( 𝑛 = 0.5, 𝜆CY = 1.0 , Re = 100)

 

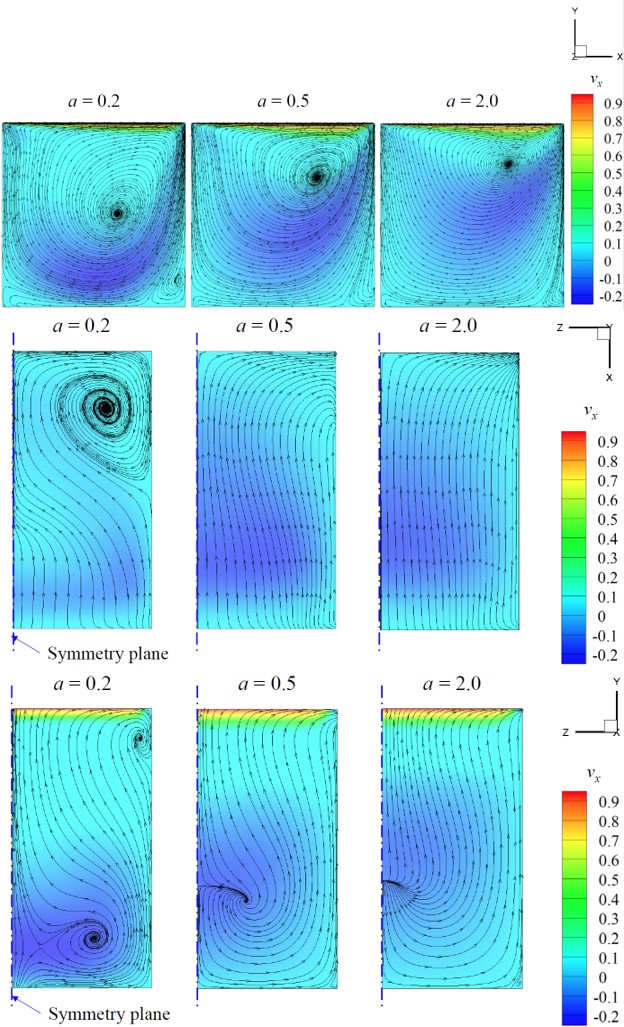
namhee-8

Fig. 3. Effect of the shape parameter, a, on streamlines on each plane ( 𝑛 = 0.5, 𝜆CY = 1.0 , Re = 100)

 

Flow over a backward-facing step

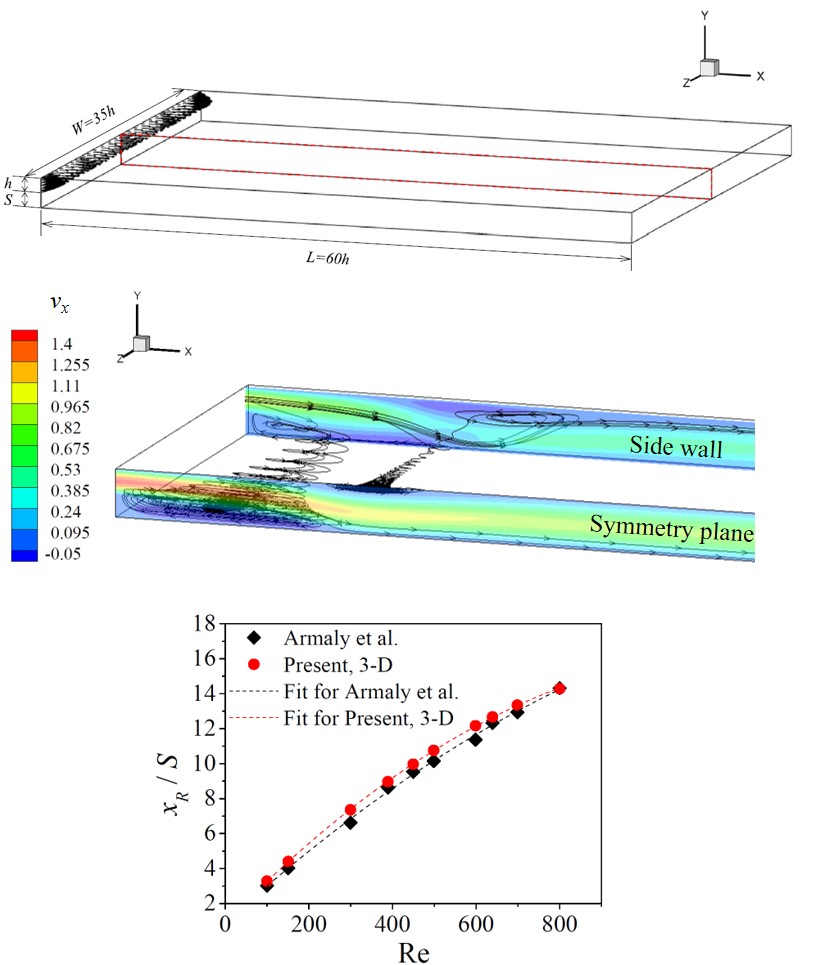
namhee-8

Fig. 1: Numerical result of the reattachment length compared with the experimental result by Armaly et al. (1983)

 

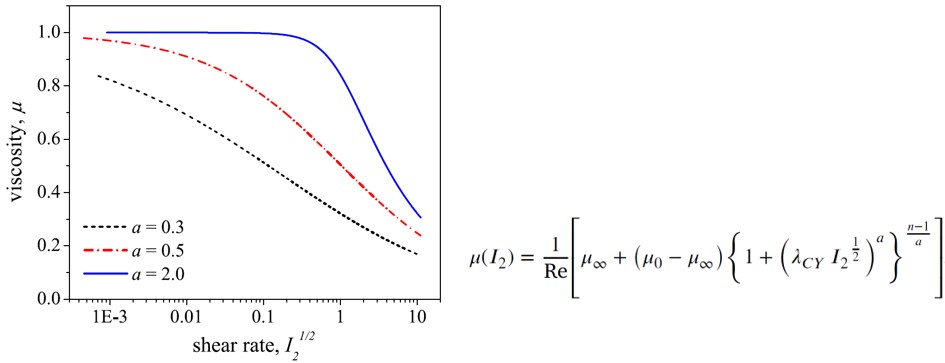
namhee-8

Fig. 2. Effect of the shape parameter, a, on the viscosity ( 𝑛 = 0.5, 𝜆CY = 1.0 , Re = 100)

 

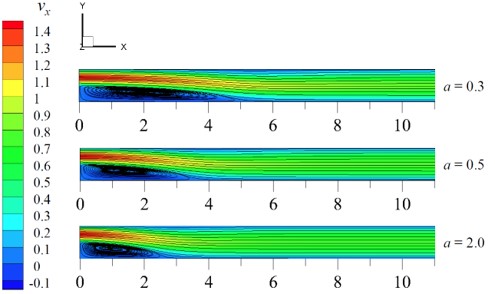
namhee-8

Fig. 3. Effect of the shape parameter, a, on streamlines on each plane ( 𝑛 = 0.5, 𝜆CY = 1.0 , Re = 100)

 

SUMMARY

  • Formulation of a mixed least-squares finite element model (LSFEM) using high-order spectral/hp approximation functions for 2D steady flows of generalized-Newtonian fluids which obey the Carreau-Yasuda viscosity model.
  • Numerical example to validate the present numerical model.
  • Different effects of the parameters of Carreau-Yasuda model on flow kinematics.

ACKNOWLEDGEMENT

The authors gratefully acknowledge the support from the Oscar S. Wyatt Endowed Chair account.

REFERENCE

1. Armaly, B. F., et al. “Experimental and theoretical investigation of backward-facing step flow.” Journal of Fluid Mechanics 127 (1983): 473-496.
2. Kim, Namhee, and J. N. Reddy. “A spectral/hp least‐squares finite element analysis of the Carreau–Yasuda fluids.” International Journal for Numerical Methods in Fluids (2016).