FINITE ELEMENT ANALYSIS OF BEAMS AND PLATES BASED ON COSSERAT CONTINUUM FOR CONSTRAINED MICRO-ROTATION
ABSTRACT
Weak form finite element models for bending of beams and plates, considering moderate rotation, are developed. The models are based on Cosserat continuum for constrained micro-rotation (rotation gradient dependent theory). A general higher order beam, 3D beam, and plate theories are presented in which the displacement fields are taken as Taylor’s series expansions about the displacements of the middle plane. Also a model for nanoindentation on CNT reinforced hard coating above elastic substrate is presented by mixed FE model using rotation gradient dependent theory . Effect of material length scale parameter are also studied.
INTRODUCTION
With the technological advances of manufacturing of small-scale structures of the various man-made materials, non-classical or generalized continuum models have gained enormous attention in the recent times, because the response of such materials defies the classical continuum mechanics approach due to either their structural length scale or small scale material embedding. These materials include fibrous composites, carbon nanotube-reinforced coatings, granular solids, liquid crystal elastomers, polarization inertia in ferroelectrics, and intrinsic spin in ferromagnetic, etc. Following the pioneering work of Cosserat brothers [1] almost a century ago, many researchers have contributed to this field. Very recently, Srinivasa and Reddy [2] have developed a model for Cosserat continua in the case of large deformation and finite constrained micro-rotation. The potential energy for this case can be written as follows: ![]() , where
, where ![]() and
and ![]() are the Cauchy Green stretch tensor and orthogonal rotation tensor, respectively.
are the Cauchy Green stretch tensor and orthogonal rotation tensor, respectively.
GENERAL HIGHER ORDER BEAM AND PLATE THEORIES
Based on the above rotation gradient dependent theory, a general higher order beam, plate, and 3D beam theories are developed in case of the von Kármán geometric nonlinearity (see [3,4]). The displacement fields considered are general power (Taylor’s) series expansion about the displacements of the mid-plane:
![]()
(1) 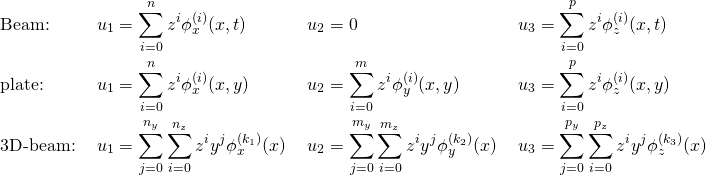
where ![]() ,
, ![]() , and
, and ![]() . All the
. All the ![]() are unknown dependent variables.
are unknown dependent variables.

RESULTS
Nonlinear FEM result of microstructure dependent beam
Dimensionless transverse displacement, moment, and various stresses of homogeneous and functionally graded (![]() ) beams are plotted for various values of length scale [3].
) beams are plotted for various values of length scale [3].

Nonlinear FEM result of microstructure dependent plate
Dimensionless transverse displacements (![]() ) and stresses (
) and stresses (![]() ) of homogeneous plate are plotted for various values of the length scale parameter ( see [4] for details).
) of homogeneous plate are plotted for various values of the length scale parameter ( see [4] for details).

Nonlinear FEM result of microstructure dependent 3D Beam
Due to ordered orientation of microstructure in Cosserat solid (e.g., liquid crystal elastomers), the structure shows resistance to various curvatures; for example, anticlastic curvature could be suppressed due to the microstructure oriented along the width of the beam and can be modelled by the 3D beam theory presented here.

Deformed thick beam due to end moment showing anticlastic curvature
APPLICATION: Modeling of Nano-indentation on CNT reinforced hard coating on elastic substrate
Because of its high strength, CNT are used as reinforcements in composites materials, which can be used as surface coatings. Because the CNT strands are very small and stiff, we can treat those as rigidly rotating embeddings and the rotation gradient elasticity can be applied. We model nanoindentation on such coatings above elastic substrate by a mixed FE model. Adhesive contact is assumed between substrate and coating but the horizontal friction forces between them are neglected [5].


Schematic diagram for the indentation on CNT reinforced hard coating on elastic substrate.


Transverse deflection due to indentation (linear analysis) (substrate- Aluminium, coating- Al with CNT reinforcement).
CONCLUSIONS
- The stiffening effect, due to the potential energy term, which depends on the rotation gradient and the classical strain energy term, is observed in case of beams and plates, and parametric studies have been carried to see the effect of different material length scale parameter values.
- Also the anisotropic response is observed in case of plates for different material length scale parameters in different directions owing to different shape and orientation of the microstructures embedded in the material.
- Non-zero skew symmetric part of stress tensor and third order couple stress tensor come into play due to the rotation gradient dependent potential energy terms.
- Also, surface tension like term comes into play at the boundary in solids (see [2-4] for details).
ACKNOWLEDGEMENTS
The financial support from the National Science Foundation Grant CMMI-1000790 and the Oscar S. Wyatt Endowed Chair funds at Texas A&M University are gratefully acknowledged.
REFERENCES
[1] E Cosserat and F Cosserat. Theorie des corps deformables. Paris, 1909.[2] AR Srinivasa and JN Reddy. A model for a constrained, finitely deforming, elastic solid with rotation gradient dependent strain energy, and its specialization to von karman plates and beams. Journal of the Mechanics and Physics of Solids, 61(3):873-885, 2013.
[3] A Arbind, JN Reddy, and AR Srinivasa. Nonlinear analysis of beams with rotation gradient dependent potential energy for constrained micro-rotation. In review (2016).
[4] A Arbind, JN Reddy, and AR Srinivasa, Nonlinear analysis of plates with rotation gradient dependent potential energy for constrained micro-rotation. In review (2016).
[5] Bakshi, S. R., Singh, V., Balani, K., McCartney, D. G., Seal, S., & Agarwal, A. (2008). Carbon nanotube reinforced aluminum composite coating via cold spraying. Surface and Coatings Technology, 202(21), 5162-5169.
