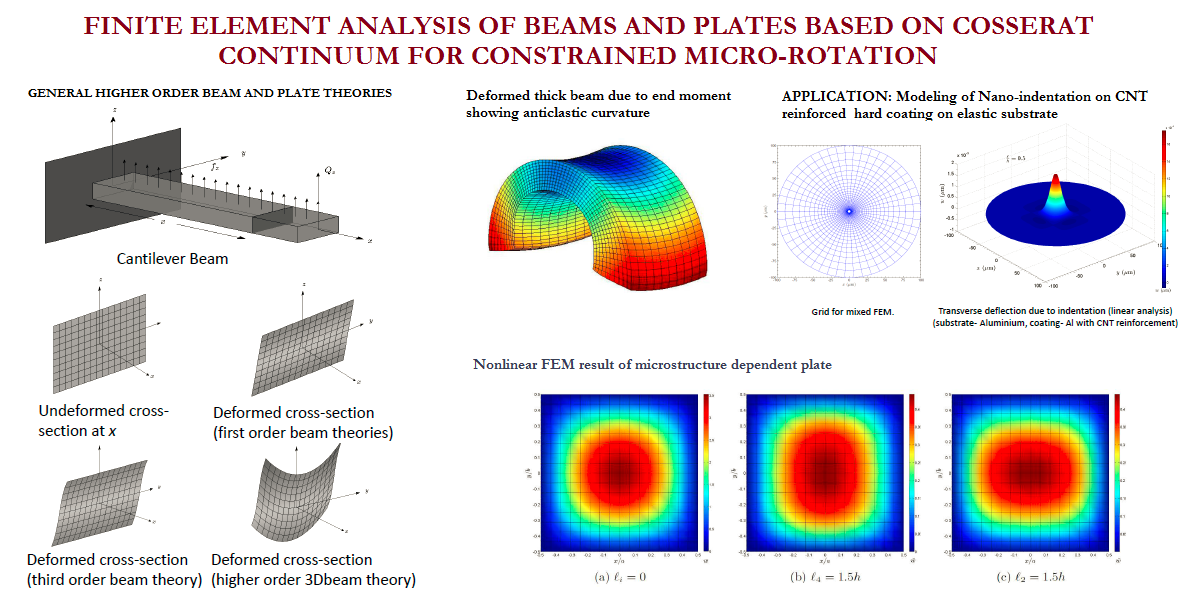
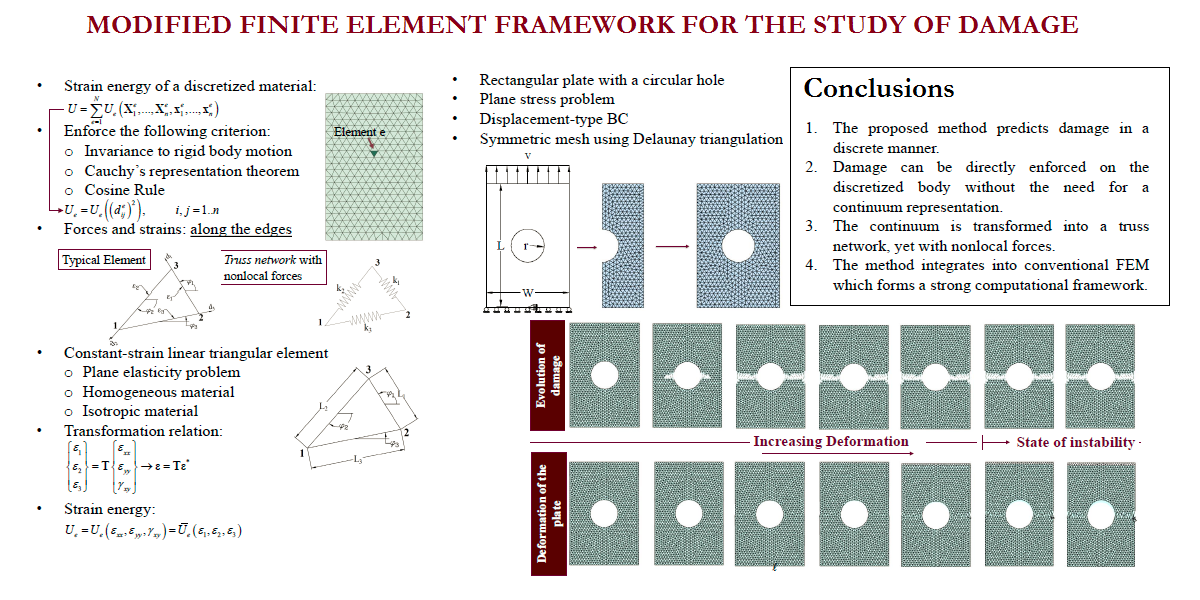
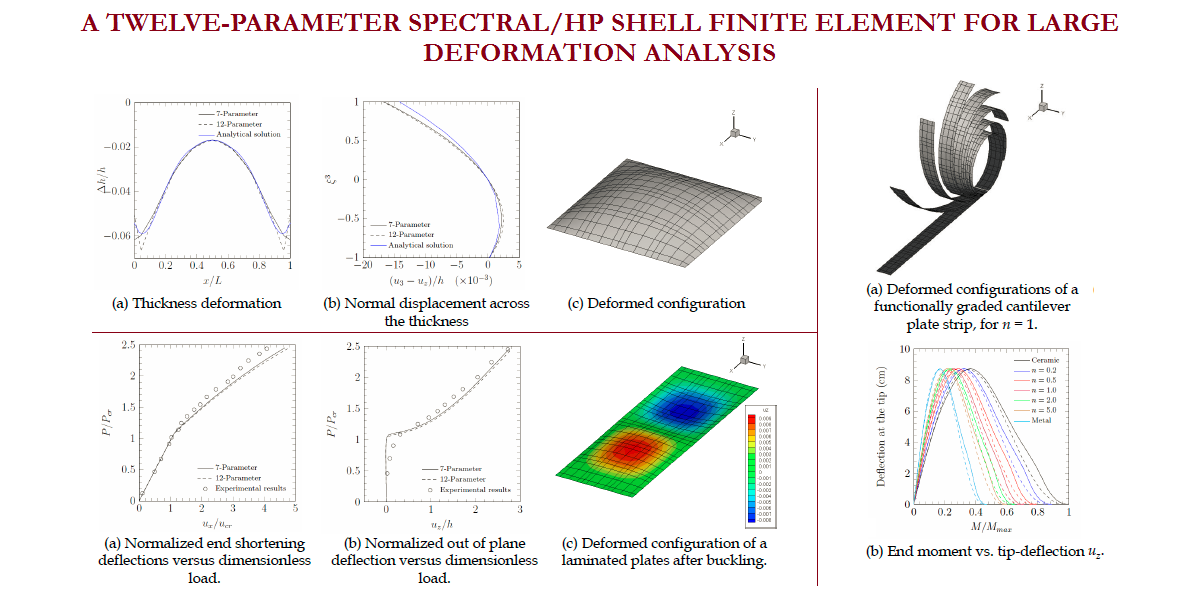
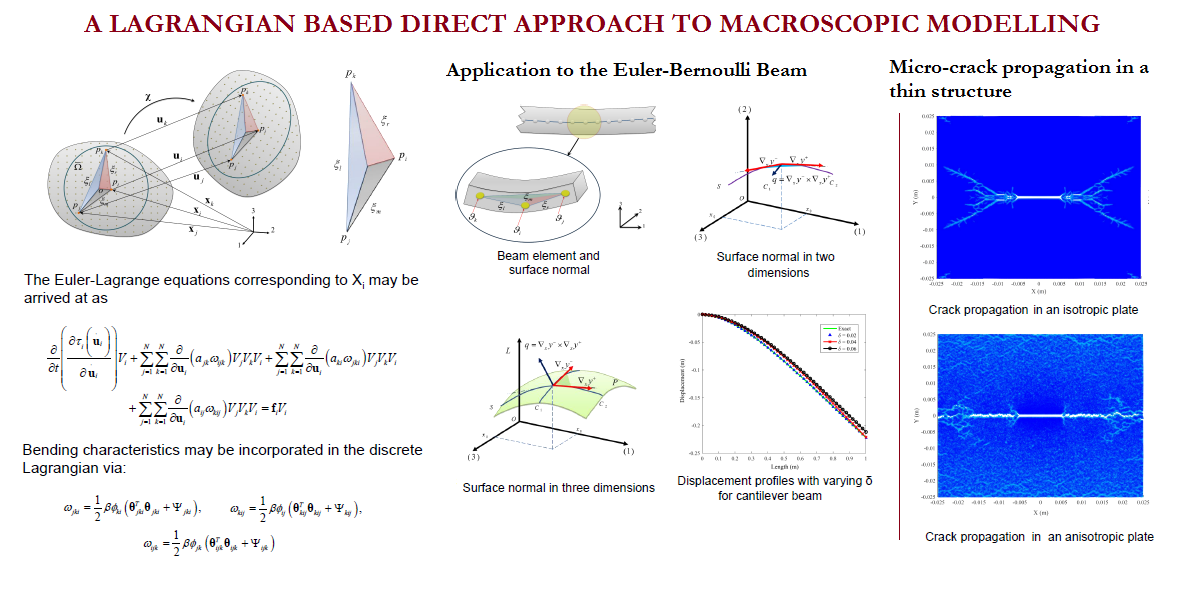
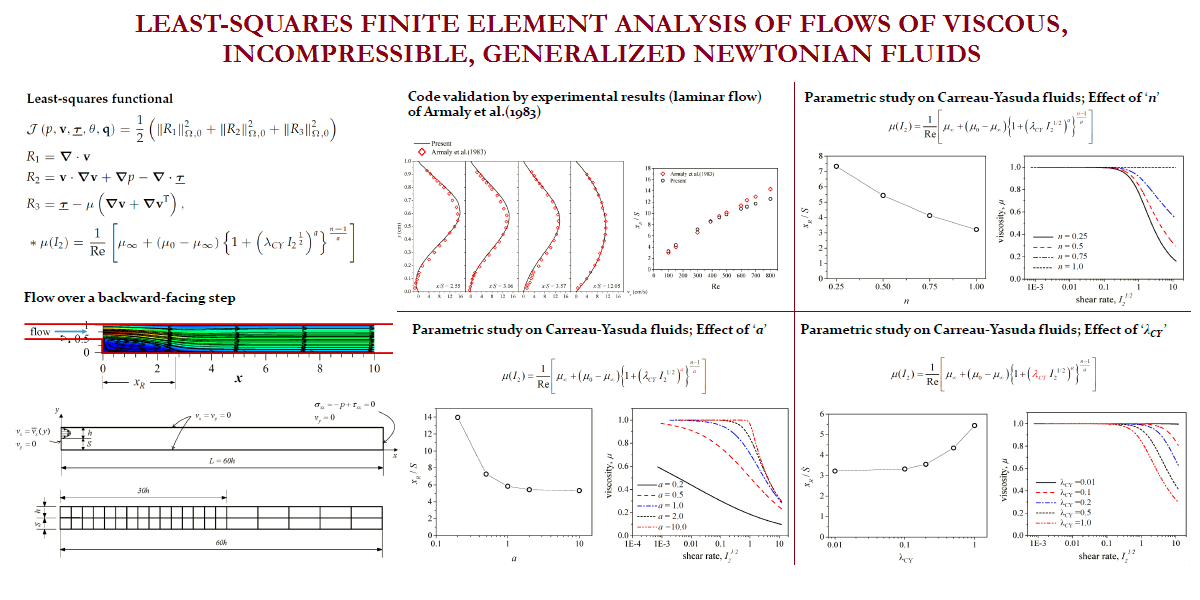
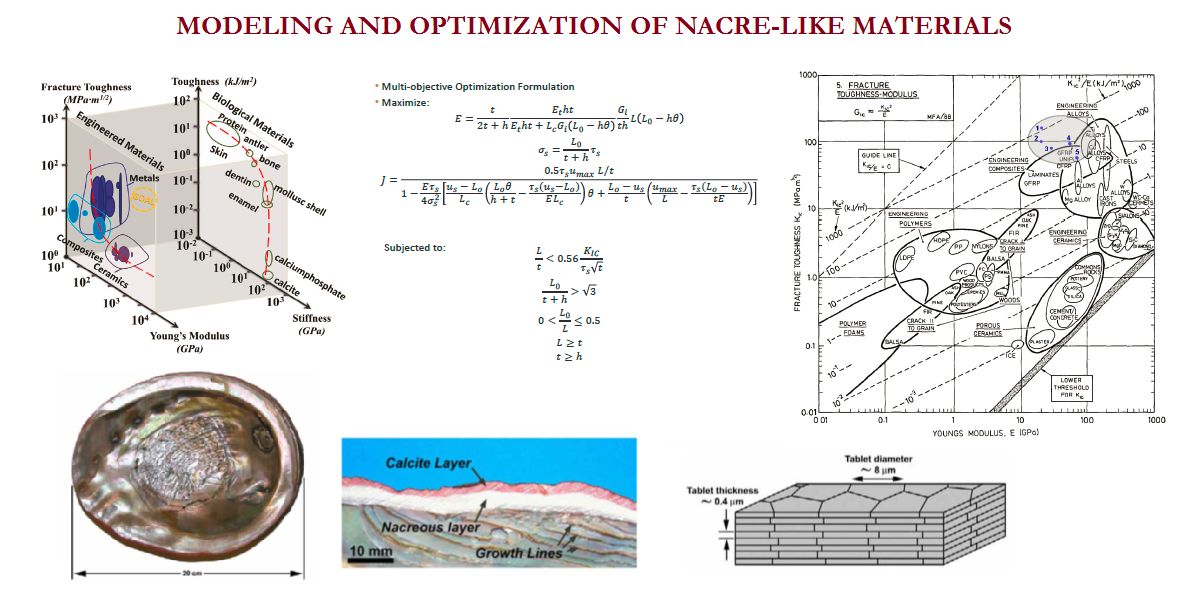
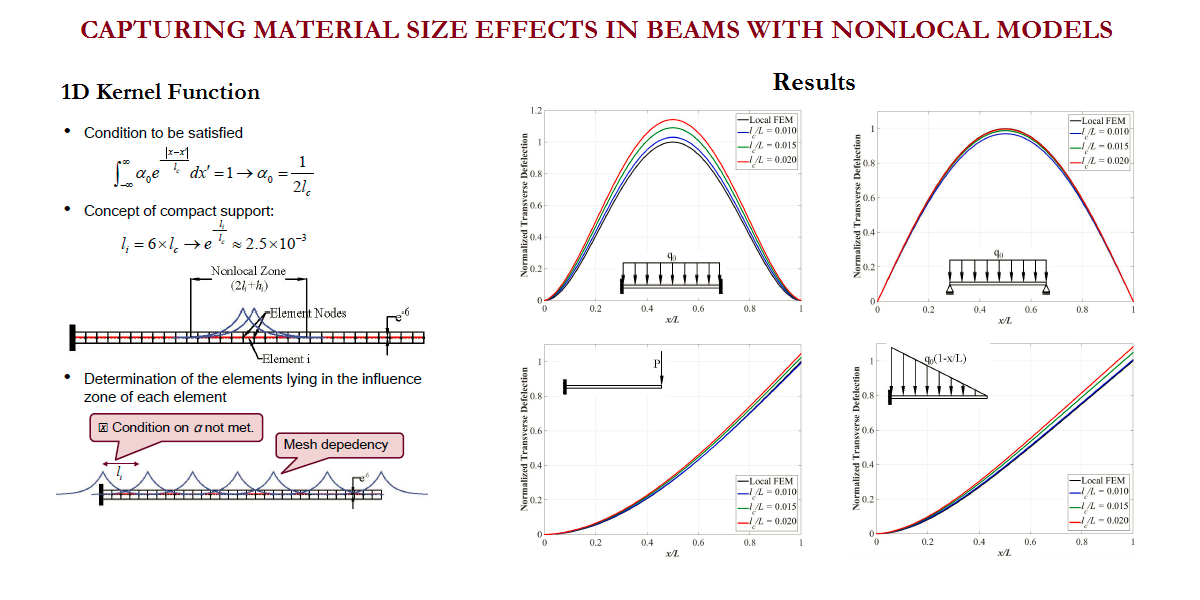
Welcome to TAMU MECHANICS and the Advanced Computational Mechanics Laboratory (ACML), which is dedicated to state-of-the-art research in the development of novel mathematical models and numerical simulation of a variety of physical phenomena. In recent years, our group pioneered practical development of least-squares based finite element models for boundary and initial value problems; 7- and 12-parameter shell theories and their finite element models using spectral approximations; nonlocal beam and plate theories using the ideas of Eringen, Mindlin, and Koiter for the modeling of mega structures and architected materials and structures; an edge-based finite element approach (GraFEM) for study of damage and fracture in brittle materials; and a dual mesh finite (control) domain method that exploits the desirable features of the finite element method and the finite volume method. The group also developed thermodynamically based strain gradient elasticity theory and internal polar continuum theories in which varying internal rates of rotations and conjugate moments are incorporated in the derivations of the conservation and balance laws. For additional details on the research projects carried out at ACML, see Research section of this website.

The TAMU MECHANICS website not only highlights the recent research works of the group, but it also contains many educational and research materials and source codes of finite element and other computer programs, which may prove to be helpful to those who wish to learn and strengthen their technical background in applied mechanics in general and the finite element method and its applications in particular. Please read the disclaimers[click here] before you use the website and its contents.